要深刻理解“反函数”的概念，毫无疑问先决条件是要先理解“函数”的概念。

函数

要知道，“函数”在英文中对应的单词是 function，通常简写为 f。所谓“函数”，其实就是某一种规则，在此规则作用下，每个有意义的(允许的)输入，都会被转换为唯一确定的一个输出。

由所有有意义的(允许的)输入值组成的集合，就是函数的定义域。而所有经规则转换后得到的输出值组成的集合，就是函数的值域。

对于函数的定义，需要理解的关键点是：

1）函数是某种特定的处理规则；

2）每个输入，经过处理后都能产生唯一的输出；

3）两个不同的输入，是可能对应同一个输出的。

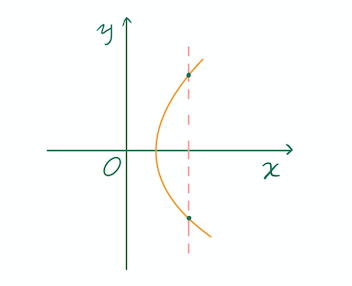
我们通常会借助图像去理解函数，有一种叫做“垂直检验”的方法，可以直观简单判断一个图像是不是函数，比如下面的图像就不是一个函数

垂直检验是否是函数 P1

垂直于x轴的虚线表明，对于同一个x的值，产生了两个完全不同的输出值。

反函数

从命名上也可以看出，反函数不是单独的存在，它是相对于“函数”的一个概念。对于某个函数 f，可以用如下的映射图表示：

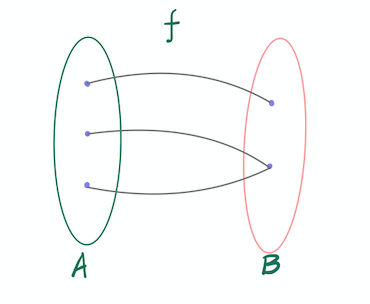
P2 函数映射定义

上图例子中，定义集合A的所有三个输入，经过函数f转换后，对应了含两个元素的值域集合B。

对于这样的函数关系，可以看成是一种正向的转换。如果将集合B的元素作为输入，是否存在函数关系 g，经过g的转换后，输出刚好是A呢？即对于B的每个元素，反向转换为A中唯一确定的一个元素。

由上图看，这样的转换是可能存在的，但P2中函数f，逆向转换时会遇到一个问题，B中的某个元素，在转换到A后，对应了两个不同的元素，这是不符合函数定义的。所以，至少说，上面P1的函数f，是不存在反向转换的。

那什么样的函数，能存在逆向的函数转换呢？不难得知，只要A的元素和B元素之间的转换满足一一对应关系就可以了。这样，我们就可以定义：对于一一对应的函数关系 f，存在一个定义在f的值域B上的函数 g，它将B作为输入，输出刚好是f的定义域A。这就是所谓反函数的定义。

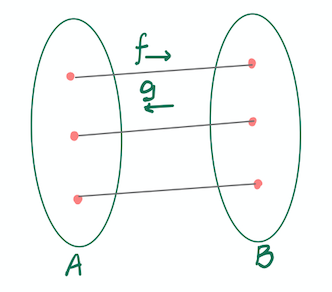
P3 反函数关系

重要提示

关于函数与反函数这对定义，重点是：

1）存在反函数的前提是一一映射；

2）一对f和g互为反函数，f的定义域是g的值域，f的值域是g的定义域；

3）f(g(x)) = x, g(f(x))=x ，经历反向的变换回到自身

4）如果知道了互为反函数的其中一个函数图像，可以简单变换得到同一坐标系下的另一个函数图像。你知道怎么做吗？