一．概念描述

现代数学：点的定义一般有以下四种：

①不可以再分割的部分。

②几何学上指没有大小（即没有长、宽、高）而只有位置，不可分割的图形。如两直线的相交处、线段的两端都是点。

③在点集拓扑中的点，定义为一个拓扑空间中的集合的元素。

④公理化定义：在几何学，拓扑学以及数学的相关分支中，一个空间中的点用于描述给定空间中一种特别的对象，在空间中有类似于体积、面积、长度或其他高维类似物。一个点是一个零维度对象。点作为最简单的几何概念，通常是几何、物理、矢量图形和其他领域的最基本的组成部分。点作为几何中最基本的组成部分，点动成线，线动成面，面动成体。点也可以看作二维上无限小的面积、三维上无限小的体积等。在平面上的点可以用一个有序数对(x，y)来表示；在n维空间中，用n个有序实数组(x1x2...xn)表示空间中的一个点。

从数学的观点看，第四个定义从零维到多维来理解点的定义最丰富、最全面。

小学数学：小学数学教材中没有明确给出点的定义，只是在认识平面图形“角，三角形、平行四边形、梯形、圆”、认识立体图形“长方体、正方体、圆锥”或给图形画高时提到了点，还有与线有关的点。这大致可以分成三种情况：

①图形的认识：角的描述就是“从一点引出两条射线组成的图形”，这“一点”就是角的顶点；三角形有三个顶点，平行四边形有四个顶点，圆锥有一个顶点。有关圆心、半径、直径的知识也都用到了点：从圆心到圆上任意一点的线段，叫作半径；通过圆心且两个端点都在圆上的线段，叫作直径。

②给图形画高：三角形的高是“从三角形的一个顶点向它的对边作一条垂线……”；平行四边形的高是“从一条边上的任意一点向对边引垂线……”；梯形的高是“从上底的任意一点向下底引垂线……”；而“从圆锥的顶点到底面圆心的距离叫作圆锥的高”。

③与线有关的点：连接两点可以画很多条线，其中线段最短，线段的长度就是这两点间的距离；过直线上或直线外一点，画已知直线的垂线或平行线等。

二．概念解读

点，表示位置，它既无长度，也无宽度，是最小的单位。在平面构成中，点的概念只是相对的，它在对比中存在。网中同一个圆点，在小的框架中会显得很大，而在巨大的框架中又会显得很小。比如，人类居住的地球与我们人类相比较是巨大的，但与宇宙相比较，它又是一个渺小的点，因此，点的概念是由相互比较的关系决定的。

几何学中的点，只有具体位置，而无大小（即没有长短、宽窄、薄厚），常用大写字母A、B、C……表示。从几何定义思考点和线是人们在解决实际问题的时候建立的一种模型，理论上的点和直线是不存在的。

点无大小，为什么线段却有长度？举个例子来解释这个问题：对于一根长度为1的线段，我们把它均分为n份，则每份的长度等于1/n。当n趋于无穷大时，1/n是趋于0的，这个长度是忽略不计的，这趋于0的每一份线段我们把它称之为点。无穷小乘无限大可以等于任何数，因此，虽然点是没有大小的，但线段是可以有长度的。

三．教学建议

(1)点的意义非常丰富，可以从零维、一维、二维、三维……n维来理解，点是几何图形最基本的、不可再分的元素。

如在一节课中认识点，线，面，教师可让学生通过触摸实物，感悟基本图形点，线，面，并由实物抽象出几何图形，提高其观察、想象与分析能力。

教师也可利用课件演示线是由无数个点组成的，无数个点的排列分布不同会形成不同的线；还可以让学生进一步理解面上也有无数个点。

此外，教师还可以专门引导学生认识平面图形和立体图形中特殊的点，如线段的端点、分点，圆的圆心，平面图形和立体图形的顶点等。

(2)点的趣味知识：长线段上的点与短线段上的点同样多

线段的长度是有限的，但无论是长线段还是短线段，它们上面点的个数却是无限的，并且长线段与短线段上的点都构成一个无穷的点的集合。对于两个集合A和B，如何比较其大小和多少呢，也就是怎样确定A中的元素多还是B中的元素多，这就需要有个标准。对于有限集合大小的比较，我们可以采用“数一数”的办法，对下无限集合就看我们能不能在A与B两个集合的元素之问建立起一种一一对应的关系。能建立一一对应的关系，就应当承认集合A和B的元素是一样多的。其实“数一数”的办法也是一一对应的办法，只不过是把要数的元素与自然数间建立一一对应罢了。

按照一一对应的原则，不同长短两条线段上的点是一样多的。例如，线段AB和线段CD上的点只要通过如图1的办法就可以建立一一对应的关系，所以线段AB和线段CD上的点是一样多的。类似的，我们还可以得到半圆周上的点和直径上的点一样多（如图2）；更进一步还可以得到，半圆周上的点还和无限长直线上的点一样多（如图3），由此，我们还能得出1毫米线段上的点和无限长的直线上的点也是一样多。所以无论多么短的一条线段，只要它的长度不是0，它上面的点就和任意长度的线段乃至无穷直线上的点一样多。

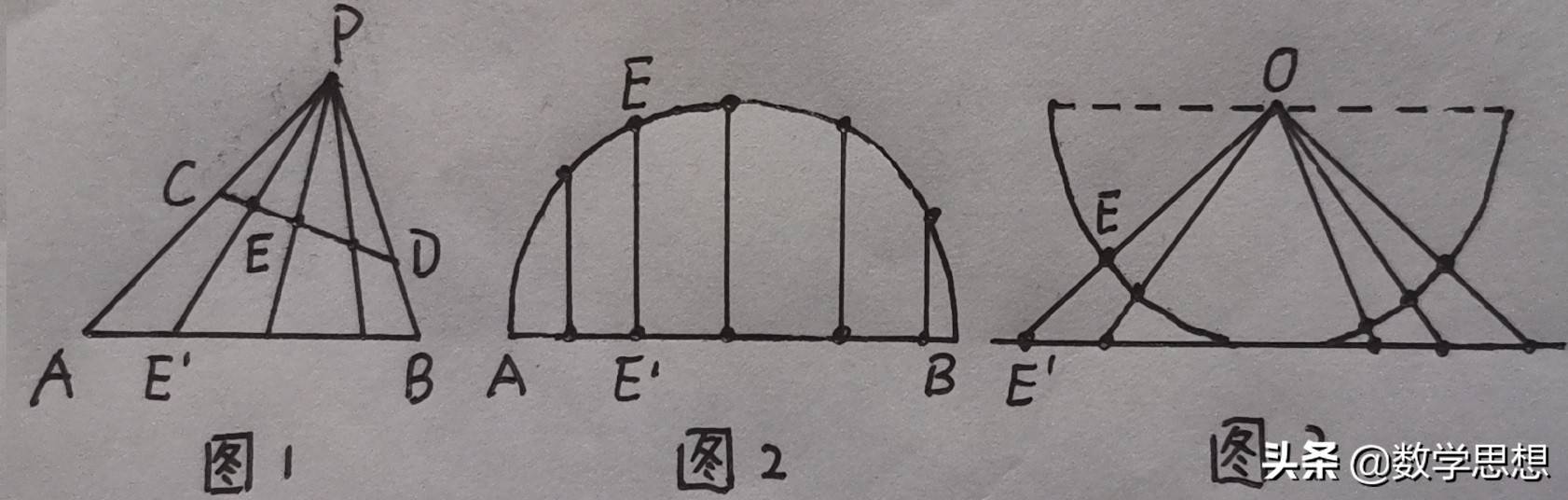
出现这种令人称奇的结果，是由于几何里的“点”，只有位置，没有大小、长短、宽窄和薄厚，而且任何一条线段或直线上的点都是无限多的，这些点都非常紧密地排列在线段和直线上，没有一点空隙。

四．推荐阅读

(1)《几何原本》（欧几里得，江苏人民出版社，2011）

该书的第一卷有关于点的概念的详细描述。

(2)《小学数学中最易误解的概念》（范立瓅，高荆，地质出版社，2008）

该书第209-210页“图形与几何”章节的“图形认识”部分，对直线，射线和线段三者之间的关系以及点，线，面，体的概念有比较详细的阐述。